Ératosthène (c. 276-195 av. J.-C.) était un astronome, géographe, mathématicien et poète grec, surtout connu pour avoir été le premier à calculer la circonférence de la Terre et son inclinaison axiale. Il est également reconnu pour son innovation mathématique, le crible d'Ératosthène, qui identifiait les nombres premiers, et pour sa position de chef de la bibliothèque d'Alexandrie.
Il était originaire de Cyrène, en Afrique du Nord (aujourd'hui Shahhat, en Libye), un centre de commerce grec prospère sur la côte de la mer Méditerranée. Jeune homme, il fut envoyé à Athènes pour étudier à l'Académie de Platon sous la direction d'Arcésilas (c. 316-240 av. J.-C.) qui avait institué le système du scepticisme académique à l'école. Le scepticisme académique encourageait les gens à remettre en question ce qui constituait la "connaissance" et à tester eux-mêmes les conclusions acceptées sur le monde plutôt que de répéter ce que d'autres avaient prétendu être la vérité. On pense que ce cours influença les travaux ultérieurs d'Ératosthène.
Il fut appelé à Alexandrie, en Égypte, par Ptolémée III Evergète (r. de 246 à 222 av. J.-C.) comme conservateur en chef de la célèbre bibliothèque de cette ville. C'est là qu'il fit ses calculs sur la circonférence de la terre et qu'il écrivit ses œuvres les plus connues, dont un ouvrage en trois volumes sur la géographie, auquel on attribue la paternité de ce terme. Il était l'ami de l'inventeur et mathématicien Archimède (287 à 212 av. J.-C.) et tous deux recommandèrent leurs travaux respectifs.
Alors qu'Archimède se concentrait sur la physique, l'astronomie et les innovations en matière d'ingénierie, Ératosthène s'intéressait à tout ce qui l'intéressait. Cela lui valut le surnom de Bêta (deuxième lettre de l'alphabet grec), car il était le deuxième meilleur dans tous les domaines, mais en même temps, il était acclamé pour ses différents travaux comme l'aurait été un vainqueur olympique. À quatre-vingts ans, il commença à perdre la vue et, estimant qu'il n'avait plus de raison de vivre, il se laissa mourir de faim. On se souvient de lui comme de l'un des plus grands polymathes de l'Antiquité et nombre des conclusions auxquelles il était parvenu et des termes qu'il avait inventés sont encore utilisés aujourd'hui.
Vie et éducation
Ératosthène, fils d'un certain Aglaos, vit le jour à Cyrène, colonie grecque établie en Afrique du Nord en 631 avant notre ère. Elle devint très vite un port de commerce prospère, s'imposant comme une république au milieu du Ve siècle avant J.-C., jusqu'à ce qu'elle ne soit prise par Alexandre le Grand. Après la mort d'Alexandre en 323 avant J.-C., elle fut dirigée par la dynastie ptolémaïque d'Égypte et, l'année de la naissance d'Ératosthène, elle déclara son indépendance. Elle fut ramenée sous le contrôle des Ptoléméens en 246 avant J.-C. par Ptolémée III, alors qu'Ératosthène était encore à Athènes où son père l'avait envoyé pour recevoir une éducation.
Athènes, à cette époque, était le centre intellectuel de la Méditerranée et l'Académie de Platon l'un des établissements d'enseignement les plus prestigieux. Eratosthène étudia sous la direction d'Arcésilas, un philosophe qui encourageait la discipline philosophique du scepticisme formulée pour la première fois par Pyrrhon d'Élis (c. 360-c. 270 av. J.-C.). Pyrrhon ne mit rien par écrit, mais son système fut préservé par son élève Timon de Phlionte (c. 320-c. 235 av. J.-C.) et développé par d'autres jusqu'à ce qu'Arcésilas n'institue ses principes en tant que principe directeur de l'Académie.
La philosophie de Pyrrhon soutenait que les gens étaient se rendaient la vie difficile car ils faisaient confiance aux perceptions sensorielles et croyaient que les conclusions basées sur celles-ci constituaient la réalité. Il n'est pas clair si Pyrrhon pensait que la réalité objective était inconnaissable ou simplement que les humains n'avaient pas la capacité de la connaître, mais dans tous les cas, le résultat pratique était le même : les perceptions sensorielles d'une personne étaient incapables de rendre la vérité sur les phénomènes observables et donc, pour obtenir la paix de l'esprit, il fallait éviter de porter des jugements ou de tirer des conclusions définitives sur le monde des sens.
Le mieux que l'on puisse faire, selon Pyrrhon, c'est de ne pas s'engager dans une conclusion, quelle qu'elle soit, de mettre en balance les raisons pour et contre son acceptation et de s'en tenir là. En agissant ainsi, on atteignait un état d'esprit connu sous le nom d'ataraxie, c'est-à-dire l'absence de détresse psychologique et de contrariété personnelle. À l'époque d'Arcésilas, la philosophie de Pyrrhon s'était développée pour se centrer sur l'affirmation que la connaissance était impossible parce que les humains étaient incapables d'appréhender le monde sensible par la perception des sens. Puisque l'on ne pouvait pas savoir ce que l'on ne savait pas, et que ce que l'on savait était limité à des perceptions sensorielles peu fiables, on ne pourrait jamais savoir ce que l'on ne savait pas ou si ce que l'on savait était, en fait, vrai.
Ératosthène et le scepticisme
Il n'existe aucune trace du séjour d'Ératosthène à Athènes ni de ce qu'il aurait étudié, mais il aurait été exposé à ce modèle philosophique à l'Académie. Bien qu'il ne soit pas considéré comme un philosophe sceptique, ses travaux ultérieurs suggèrent qu'il suivit le paradigme sceptique essentiel consistant à refuser d'accepter les conclusions des autres, à rejeter les impressions des perceptions sensorielles et à tenter de trouver la vérité sur un sujet donné par des applications raisonnées. Le philosophe sceptique et compilateur Sextus Empiricus (c. 160-c. 210 ap. J.-C.) définit les principes sceptiques qui semblent avoir inspiré les vues et la méthodologie d'Ératosthène :
Car les grands génies, qui ont été les auteurs de cette discipline, voyant que cette égalité de raisons qu'ils remarquaient dans les choses, les troublait, ils commencèrent à examiner ce qu'il pouvait y avoir de vrai ou de faux dans les choses; afin de se procurer une disposition exempte de trouble, par le discernement qu'ils feraient de ces choses. Mais si on demande le principe sur lequel le sceptique se fonde principalement pour douter de tout, c'est celui-ci: Que toute raison peut être contredite par une raison opposée d'un poids et d'un moment égal. Ce principe-là nous conduit à reconnaître qu'il n'y a aucun dogme, rien que l'on ne puisse affirmer ou nier dogmatiquement et avec assurance. (I.VI.12)
Accepter les dogmes comme des vérités, selon le scepticisme, enfermait l'individu dans une mentalité établie qu'il se sentait alors obligé de défendre au lieu de la remettre en question. En restant sceptique à l'égard de tout dogme, on était libre d'explorer le sujet par soi-même, par la raison. En suivant cette voie, on pouvait ne pas savoir ce que l'on ne savait pas, mais on pouvait au moins savoir que ce que l'on savait pouvait être considéré comme exact. C'est ce modèle qui semble avoir influencé les recherches d'Ératosthène sur les connaissances acquises de son époque.
Alors qu'il vivait et étudiait encore à Athènes, Ératosthène écrivit un certain nombre d'ouvrages, aujourd'hui perdus, qui furent cités par des auteurs ultérieurs et qui suggéraient une application des principes sceptiques. Parmi ceux-ci figure une série d'histoires, les Chronographies, qui recalculait les dates importantes de l'histoire en commençant par la guerre de Troie, et qui était considérée comme plus précise que les travaux précédents. Un autre de ses ouvrages traitait des aspects mathématiques de la philosophie de Platon, démontrant peut-être comment les affirmations philosophiques pouvaient être prouvées mathématiquement, bien qu'il ne s'agisse que de spéculations, l'ouvrage ayant été perdu. Ces travaux, ainsi que d'autres, furent portés à l'attention de Ptolémée III Evergète qui lui demanda de venir à Alexandrie pour prendre en charge le fonctionnement de la bibliothèque.
Alexandrie et la circonférence de la Terre
Les Ptolémées souhaitaient faire d'Alexandrie la rivale d'Athènes en tant que centre intellectuel et, à cette fin, ils y avaient déjà construit la bibliothèque près du grand temple du dieu Sérapis (le Sérapéum ou Sérapéon). La Grande Bibliothèque d'Alexandrie, qui contenait des milliers de parchemins, fut complétée par une seconde dans le Sérapéum, Ptolémée III ayant fait de l'acquisition de livres une priorité. Chaque navire arrivant au port d'Alexandrie était arraisonné et fouillé à la recherche de livres. Une fois trouvés, ils étaient copiés, et les copies étaient données aux propriétaires; les originaux devenaient partie intégrante de la collection d'Alexandrie. On dit que ces copies étaient si précises que l'on ne pouvait les distinguer des originaux.

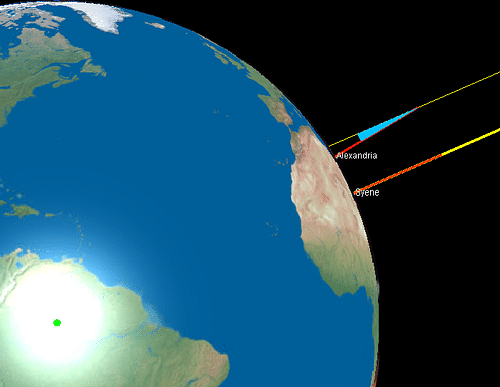
Eratosthène, en tant que bibliothécaire en chef, était responsable de l'acquisition de ces livres et de la qualité des copies et était également le tuteur des enfants de Ptolémée III. Il prit au sérieux la vision ptolémaïque d'Alexandrie en tant que grand siège du savoir, élargissant la collection de la bibliothèque et l'organisant en sections plus clairement définies. Alors qu'il vaquait à ses occupations, il entendit parler d'un puits dans la ville de Syène (aujourd'hui Assouan), au sud, dont l'eau (et non les parois du puits) était entièrement illuminée par le soleil à midi au solstice d'été (vers le 21 juin), ce qui suggérait que le soleil était directement au-dessus de la tête. Il observa que, le même jour, les obélisques et d'autres objets à Alexandrie projetaient de longues ombres et comprit qu'en calculant la distance entre les deux villes et l'angle du soleil, il pouvait trouver la circonférence de la terre.
Vers 240 avant Jésus-Christ, il érigea un mât à Alexandrie et engagea un homme pour parcourir à pied la distance entre Alexandrie et Syène afin de la mesurer (bien qu'elle fût déjà connue grâce aux caravanes commerciales). Une fois qu'il sut que la distance était de 5 000 stades (500 miles/800 km), il mesura l'angle des rayons du soleil par rapport à ce poteau (en divisant la longueur de l'ombre par la hauteur du poteau) pour un angle de 7,12 degrés. Les Grecs savaient déjà que la terre était ronde et la considéraient comme un cercle de 360 degrés. En divisant 360 par 7,2 (pour que 360 soit divisé de manière égale), il arriva à une circonférence de la terre de 250 000 stades (environ 24 854 miles/40 000 km). Ératosthène publia ses conclusions dans son ouvrage intitulé De la mesure de la Terre, qui n'existe aujourd'hui que sous forme de fragments dans les œuvres d'autres auteurs, à commencer par l'astronome Cléomède, dont le texte constitue la base de ceux qui suivirent.
Ses calculs furentent généralement considérés comme exacts et le géographe Strabon (64 av. J.-C. - v. 24 ap. J.-C.), dans sa Géographie, note que, même si ce n'était pas le cas pour tout le monde par la suite, les calculs d'Ératosthène continuaient à être considérés comme fiables et étaient encore utilisés à l'époque de l'astronome Hipparque de Nicée (190 à 120 av. J.-C.) :
Ce qu'il dit en commençant de la nécessité d'introduire dans la géographie les hypothèses reçues en mathématique et en physique est juste, et il a raison de poser en fait que, si la terre, comme l'univers lui-même, a réellement la forme sphérique, la partie habitée de la terre figurera aussi un cercle; sur mainte autre proposition semblable, il a raison également. En revanche, ce qu'il dit de la grandeur de la terre est contesté par les géographes venus après lui, et la mesure qu'il en a donnée n'a pas été généralement ratifiée, bien qu'Hipparque, dans le travail où il note les apparences célestes pour chaque lieu, se soit servi des distances mêmes mesurées par Ératosthène sur le méridien de Méroé, d'Alexandrie et du Borysthène, en déclarant qu'elles différaient peu de la vérité. (Livre I.4.1, trad. A. Tardieu)
Strabon commente ici l'œuvre en trois volumes d'Ératosthène, Géographie, qui cherche à dresser une carte précise du monde. Le premier volume critiquait l'Odyssée d'Homère, qu'il jugeait absurde du point de vue géographique, car les différentes terres qu'Ulysse était censé avoir visitées étaient beaucoup plus proches les unes des autres qu'elles n'étaient décrites. C'est également dans ce volume que le terme "géographie" fut inventé et que le sujet fut pour la première fois abordé. Le deuxième volume contenait, entre autres, les étapes du calcul de la circonférence de la terre, et le troisième volume aurait détaillé les différentes terres habitées et commenté les peuples qui s'y trouvaient.
Strabon, en commentant l'ouvrage, note comment Ératosthène s'opposa au sentiment de supériorité des Grecs sur les autres, affirmant que tous les gens devraient être jugés sur leurs mérites individuels, et non sur leur race, leur ethnie ou leur nationalité:
Pour terminer maintenant la présente série de ses Mémoires, Ératosthène rappelle que certains auteurs ont proposé une autre division du genre humain en deux groupes, à savoir les Grecs et les Barbares; mais, loin de l'adopter, il la compare à ce conseil donné naguère à Alexandre par quelques-uns de ses courtisans, de traiter tous les peuples grecs en amis et en ennemis tous les peuples barbares, et érige en principe que la seule division possible à établir entre les hommes est celle qui a pour base le bien et le mal. (Livre I.4.9)
La Géographie d'Ératosthène, comme ses autres œuvres, fut également perdue, mais elle était considérée comme une réalisation intellectuelle importante dans l'Antiquité, ainsi que controversée, car elle remettait en question la vision homérique du monde, que beaucoup considéraient comme une vérité irréfutable. Cependant, conformément à son éducation sceptique, Ératosthène refusa d'accepter la compréhension populaire de tout sujet et chercha toujours à découvrir la vérité par lui-même.
Crible d'Ératosthène
Un exemple de cela est son algorithme connu sous le nom de "criblr d'Ératosthène", qui permet de localiser les nombres premiers. Un nombre premier est un nombre naturel qui n'est pas atteint en combinant deux nombres plus petits, tandis qu'un nombre composite est le produit de n'importe quel nombre plus petit. Les Grecs ne définissaient pas le chiffre 1 comme un nombre et le chiffre 2 était donc considéré le premier nombre premier. Le crible d'Ératosthène était appelé ainsi parce qu'il agissait comme un crible pour séparer les nombres premiers des nombres composés. En commençant par le nombre 2, les multiples des nombres composites sont révélés séquentiellement jusqu'à ce qu'il ne reste plus que des nombres premiers dans le "crible". Cette innovation permit de faciliter et de rendre plus efficaces les calculs mathématiques.
On dit également qu'il écrivit des ouvrages sur l'art dramatique et le théâtre en général, l'éthique, l'astronomie, et qu'il cartographia le Nil plus précisément et plus loin que quiconque avant lui. Il est également connu pour avoir créé un calendrier qui tenait compte des années bissextiles, mais ces contributions furent toutes perdues. L'érudit T.L. Heath commente :
Dans son ouvrage intitulé De la mesure de la Terre, Eratosthène aurait discuté d'autres questions astronomiques, de la distance des cercles tropiques et polaires, de la taille et de la distance du soleil et de la lune, des éclipses totales et partielles, etc.
Véritable polymathe, Ératosthène aurait contribué de manière significative à de nombreux domaines et disciplines différents avant que sa vue défaillante ne le conduise à mettre fin à ses jours. Bien qu'on lui ait attribué le surnom de Bêta - l'équivalent de l'expression "touche-à-tout" de nos jours - sa réputation d'excellence dans de nombreux domaines différents suggère qu'il s'agissait plus d'une plaisanterie que de quelque chose à prendre au sérieux.
Conclusion
Bien que ses travaux aient été très appréciés, ils n'en furent pas moins contestés et ses calculs de la circonférence de la Terre furent retravaillés par l'astronome Posidonios de Rhodes (c. 135 - c. 51 av. J.-C.). Le système de Posidonios était considéré comme plus facile à utiliser et plus proche des dimensions proposées par Aristote (384 à 322 av. J.-C.), qui était considéré comme la norme par laquelle toute affirmation était mesurée.
Les calculs de Posidonios aboutirent à une circonférence de la Terre plus petite mais, parce qu'ils étaient devenus plus populaires que ceux d'Ératosthène, ils furent utilisés dans l'ouvrage le plus vendu, l'Almageste de l'astronome Ptolémée (100 à 170 de notre ère), qui continuerait à exercer une influence considérable jusqu'à la Renaissance européenne. Bien que les calculs d'Ératosthène aient toujours été utilisés, le système de Posidonios était considéré comme valide du fait de son inclusion dans l'ouvrage de Ptolémée. Ce sont les calculs de Posidonios que Christophe Colomb (1451 à 1506) utilisa pour convaincre ses mécènes de le parrainer, car il était en mesure de leur montrer la brièveté d'un voyage à travers l'océan Atlantique.
Le système d'Ératosthène était toutefois plus précis et fut utilisé par de nombreux capitaines de navires et cartographes européens de manière efficace tout au long de l'Âge des grandes découvertes. De nos jours, on considère que les calculs d'Ératosthène sont plus proches de la circonférence réelle de la Terre que ceux de Posidonios ou d'Aristote, et il est reconnu comme l'un des plus grands intellectuels de l'Antiquité.