Les mathématiques grecques, l'étude des nombres et de leurs propriétés, des modèles, de la structure, de l'espace, des changements apparents et des mesures, auraient été créées par Thalès de Milet (vers 585 av. J.-C.), mais avaient été clairement comprises pendant les périodes de la civilisation minoenne (2000-1450 av. J.-C.) et de la civilisation mycénienne (vers 1700-1100 av. J.-C.) et étaient dérivées de systèmes mathématiques mésopotamiens et égyptiens plus anciens.

Ces systèmes avaient toutefois des objectifs pratiques, comme l'a noté l'universitaire Rosalie David :
Les mathématiques servaient essentiellement à des fins utilitaires en Égypte et ne semblent pas avoir été considérées comme une science théorique. (217)
L'universitaire Gwendolyn Leick dit la même chose des mathématiques mésopotamiennes:
Les mathématiques faisaient partie intégrante de la formation et de la pratique des scribes. Des tablettes datant du début de la période dynastique démontrent que la géométrie était essentielle pour diviser les parcelles de terre à des fins d'agriculture et d'irrigation. (116)
Thalès et l'autre grand mathématicien de l'époque, Pythagore (de 571 à 497 av. J.-C., surtout connu pour son célèbre théorème), considéraient les mathématiques comme un moyen d'appréhender la vérité, les élevant du niveau d'un simple instrument pragmatique à la base de la compréhension de la réalité. Aucun des écrits de Thalès n'a survécu, mais il est considéré comme le premier mathématicien de Grèce pour avoir introduit la géométrie et, semble-t-il, pour la manière dont il l'appliqua. Pythagore, peut-être l'un de ses élèves, plaça les mathématiques au cœur de sa philosophie qui prônait, entre autres, la réincarnation, selon laquelle l'âme, comme les nombres, était éternelle et revenait après la mort sous d'autres formes et encore d'autres formes.
Parmi les élèves de Pythagore, on trouve Hippase de Métaponte (de 530 à 450 av. J.-C.), à qui l'on attribue la découverte des nombres irrationnels, et dont les travaux furent développés par Théodore de Cyrène (au Ve siècle av. J.-C.). Un autre pythagoricien, Philolaos de Crotone (de 470 à 385 av. J.-C.) développa le modèle pyrocentrique de l'univers et fut le professeur du grand mathématicien Archytas de Tarente (au Ve siècle av. J.-C.). Archytas, à son tour, fut le professeur d'Eudoxe de Cnide (de 408 à 355 av. J.-C.), également célèbre en tant que brillant mathématicien et astronome.
Ces mathématiciens influencèrent les travaux de Platon (424/423-348/347 av. J.-C.) et d'Aristote (384-322 av. J.-C.), dont les philosophies s'inspiraient des mathématiques, notamment de la géométrie. Euclide (c. 300 av. J.-C.) établit la géométrie dans ses célèbres Éléments et est connu comme le "père de la géométrie". Le mathématicien grec le plus connu est l'inventeur et ingénieur Archimède de Syracuse (287-212 av. J.-C.), mais on peut également citer Eratosthène (c. 276-195 av. J.-C.), Apollonios de Perga (c. 240 à 190 av. J.-C.), Aristarque de Samos (de 310 à 230 av. J.-C.), Hipparque de Nicée (de 190 à 120 av. J.-C.), Ménélas d'Alexandrie (vers 100 ap. J.-C.) et Claude Ptolémée (de 100 à 170 ap. J.-C.). Ces penseurs jetèrent les bases qui furent développées par les mathématiciens ultérieurs, en préservant et en faisant progresser leurs travaux, ce qui permit aux mathématiques de progresser jusqu'à l'ère moderne.
Revendication d'un héritage volé
Les Sumériens de Mésopotamie avaient déjà développé des mathématiques sophistiquées au début de la période dynastique (2900-2334 av. J.-C.) avec une notation sexagésimale de 60. Cela leur permit de créer le concept actuellement reconnu comme le "temps", basé sur le concept de 60, qui définit une minute comme 60 secondes et une heure comme 60 minutes. Le système sumérien témoigne d'une compréhension de l'addition, de la soustraction, de la multiplication, de la division, de l'algèbre, de la géométrie, des réciproques, des carrés et des équations quadratiques. Les Égyptiens, plus pratiques et conservateurs, travaillaient sur l'addition, la soustraction, la multiplication et la division avec des éléments de calcul et, peut-être, d'algèbre.
Comme nous l'avons vu, les Mésopotamiens et les Égyptiens utilisaient les mathématiques à des fins pratiques. Rosalie David précise :
Les Égyptiens possédaient certainement un système organisé de connaissances mathématiques, mais ils utilisaient l'expérience pratique plutôt que les capacités de raisonnement pour résoudre les problèmes. Bien qu'ils aient commencé par des concepts élémentaires, ils ont rapidement développé des systèmes permettant de résoudre des problèmes arithmétiques et géométriques compliqués, et ils ont utilisé des fractions. (218)
Il est donc inexact de prétendre que les Grecs inventèrent les mathématiques, bien que cette affirmation ait été avancée pendant des siècles, et il est plus précis de dire qu'ils développèrent des concepts mathématiques davantage que les civilisations précédentes. Même si les mathématiques sumériennes étaient très avancées, elles étaient loin d'être aussi raffinées que les mathématiques grecques à partir du 6e siècle avant notre ère. Le théorème de Pythagore, par exemple, était connu des Babyloniens bien avant la naissance de Pythagore, mais sa définition non seulement préserva le concept, mais semble également l'avoir affiné.

Néanmoins, l'affirmation selon laquelle les mathématiques et la philosophie grecques auraient été en quelque sorte "volées" à des civilisations antérieures est également inexacte et constitue une simplification excessive qui ne tient pas compte de l'histoire réelle. Les hiéroglyphes égyptiens et les cunéiformes mésopotamiens ne furent pas déchiffrés avant le milieu ou la fin du XIXe siècle et, à ce moment-là, un nombre important de travaux historiques avaient été réalisés par des érudits européens qui ne connaissaient l'histoire qu'à travers ce qui était à leur disposition, à savoir les sources grecques et latines. Les "décorations" relevées sur les temples, les tombes et les inscriptions de l'ancienne Mésopotamie et de l'Égypte n'étaient pas reconnues comme des systèmes d'écriture - et il était impossible qu'elles l'aient été - puisqu'elles n'avaient pas encore été déchiffrées vers 1820.
Bon nombre des conclusions auxquelles sont parvenus les érudits du début de l'ère moderne et de l'ère moderne concernant l'histoire ancienne doivent aujourd'hui être révisées - et il ne fait aucun doute que des motifs raciaux étaient à l'œuvre dans l'interprétation des données - mais, dans l'ensemble, ils n'ont pas intentionnellement écarté les civilisations antérieures pour favoriser les Grecs; ils ignoraient tout simplement l'histoire de la Mésopotamie et de l'Égypte. Si l'on croit, d'après le relevé que l'on a effectué, que sa propriété couvre un nombre X de pieds, et que l'on est ensuite informé par son voisin qu'il possède en fait ces pieds, on ne peut pas être accusé d'avoir volé la terre, mais seulement d'avoir été mal informé. Si l'on ne respecte pas la nouvelle information et que l'on n'y répond pas, c'est seulement à ce moment-là que l'on peut être considéré comme fautif.
Les mathématiques grecques, reconnues comme basées sur des systèmes antérieurs, datent donc du 6e siècle avant notre ère. Les systèmes minoens et mycéniens furent perdus pendant l'âge des ténèbres grec et ne furent pas reconstitués. Thalès de Milet est donc généralement considéré comme le premier à avoir introduit les mathématiques théoriques en Grèce, même si la discipline existait avant lui dans d'autres régions.
Philosophes présocratiques et pythagoriciens
Thalès fut le premier des philosophes présocratiques, terme qui désigne les penseurs ayant vécu en Grèce avant l'époque de Socrate d'Athènes (470/469-399 av. J.-C.), et il est donc connu comme le premier philosophe de la Grèce antique. D'après les travaux d'auteurs grecs postérieurs, il semble avoir suivi le même paradigme que les Babyloniens et les Égyptiens au début, en utilisant les mathématiques à des fins pratiques. Il aurait, par exemple, mesuré la hauteur des pyramides de Gizeh en calculant la différence entre leurs ombres et la sienne et, appliquant des principes mathématiques à un problème logistique, il aurait détourné le cours de l'Halys pour que l'armée du roi Crésus (r. de 560 à 547 av. J.-C.) puisse le traverser, alors qu'il était employé par Crésus en tant qu'ingénieur.
Avec le temps, cependant, ses mathématiques devinrent plus théoriques, car il proposa des axiomes, des preuves, définit la signification des nombres, développa la géométrie, proposa le théorème de Thalès (pour trouver le centre d'un cercle) et appliqua les mathématiques à l'astronomie, en prédisant avec précision l'éclipse de soleil du 28 mai 585 avant notre ère.
Cependant, Pythagore (un autre philosophe présocratique) développa davantage les mathématiques en tant que programme d'études. L'écrivain plus tardif Proclus (alias Proclos) note que "Pythagore a transformé la philosophie géométrique en une forme d'éducation libérale en cherchant ses premiers principes dans un domaine supérieur de la réalité" (Baird, 16). Pour Pythagore, les mathématiques étaient un moyen d'atteindre une fin, mais aussi la fin elle-même. Les premiers présocratiques se préoccupaient de trouver la cause première de l'existence, proposant l'eau, l'air, le feu ou d'autres éléments du monde, mais Pythagore affirmait que les mathématiques expliquaient le monde visible et invisible parce que les nombres, comme la création, n'ont ni commencement ni fin.
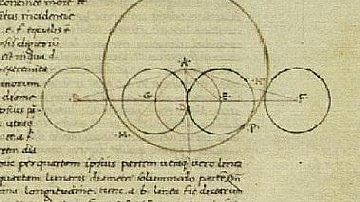
Pour Pythagore, le nombre était la cause première, car il pouvait être prouvé que le multiple pouvait provenir de l'unique - la pluralité observée dans le monde pouvait provenir, et provenait effectivement, d'une source unique. Le concept de nombre de Pythagore était basé sur un point au centre d'un cercle - la monade, qui représentait le concept de l'Un, de l'unité. De la monade naquit la dyade, deux cercles partageant désormais un centre commun et, en traçant une ligne horizontale à leur intersection, un triangle équilatéral est formé, transformant la dyade en triade, et ainsi de suite jusqu'à la décade. De l'Un est donc né le multiple et, bien que les nombres puissent sembler limités dans leur séquence de 1 à 10, ils sont en fait illimités dans les combinaisons de cette séquence de 11 à 20, puis de 21 à 30, et ainsi de suite à l'infini.
Pythagore appliqua la nature éternelle des nombres à l'âme humaine, affirmant que l'esprit d'une personne, tel un nombre, revenait sans cesse après la mort corporelle sous différentes formes - comme la séquence des nombres - apparaissant tantôt comme un être humain, tantôt comme un chien, une mule ou une mouche domestique. Pythagore prônait donc le végétarisme, car il n'y avait aucun moyen de savoir si l'animal que l'on abattait n'était pas son oncle ou son père décédé dans le corps d'un poulet.
L'élève de Pythagore, Philolaos de Crotone, rejeta ce qu'il considérait comme un non-sens d'établir une cause première et consacra son énergie à l'examen mathématique du cosmos, concluant finalement que la Terre (et toutes les autres planètes ainsi que le soleil) tournait autour d'un feu central et illimité, contredisant le modèle accepté à l'époque selon lequel la Terre était le centre de l'univers. Il rejeta l'école milésienne de Thalès et de ses disciples Anaximandre et Anaximène, qui insistaient sur l'importance de la cause première, en faveur d'une utilisation plus pratique de la philosophie pour reconnaître le fonctionnement du monde observable. L'érudit Robin Waterfield commente:
[Pour Philolaos], la véritable essence des choses n'est accessible qu'aux dieux, ou peut-être à un homme doté d'une connaissance divine; et dans la nature des choses, nous ne pouvons pas connaître l'infini. Philolaos critique ici en partie les Milésiens ou d'autres tentatives similaires visant à découvrir une réalité ultime derrière les choses de ce monde. Il suggère que c'est impossible et que le mieux que l'on puisse faire est d'essayer de dire quelles sont les conditions préalables nécessaires à l'existence du monde auquel nous sommes confrontés. (93)
Archytas adopte l'approche de Philolaos et applique également les mathématiques pour comprendre la forme du monde et son fonctionnement. En fait, on dit qu'Archytas était très admiré par Platon pour sa capacité à combiner l'idéalisme philosophique et l'application pratique. Archytas n'était pas seulement un général de Tarente, élu sept années de suite et considéré comme invincible, mais il est également connu comme le fondateur de la mécanique mathématique, célèbre pour avoir résolu le problème géométrique connu sous le nom de "doublement du cube", et fut renommé de son vivant pour ses contributions à l'astronomie et à la théorie de la musique.
Platon et Aristote
Bien que Platon ne figure généralement pas dans les listes de mathématiciens grecs, la forme sous-jacente de sa philosophie était les mathématiques et, plus particulièrement, la géométrie pure. Platon rejeta le relativisme défendu par des sophistes comme Protagoras d'Abdère (485-415 av. J.-C.), qui affirmait que "l'homme est la mesure de toute chose" - que l'individu seul définissait la vérité - et insistait sur les vérités universelles et éternelles qui déterminaient ce qui était reconnu comme la "vérité" sur terre. Pour Platon, une chose n'est pas "vraie" simplement parce qu'on la croit telle; elle est "vraie" dans la mesure où elle participe à la forme de la vérité dans un domaine supérieur. La géométrie, selon Platon, établit ces vérités supérieures, calme les passions, clarifie l'esprit et libère du "vrai mensonge" ou du "mensonge de l'âme" qui fait croire à tort aux aspects les plus importants de la vie.

Aristote (l'élève le plus célèbre de Platon), quant à lui, est connu pour ses contributions aux mathématiques grecques. L'universitaire Thomas R. Martin écrit:
Aristote considérait la science et la philosophie non pas comme des sujets abstraits isolés des préoccupations de l'existence ordinaire, mais plutôt comme la recherche disciplinée de la connaissance dans tous les aspects de la vie. Cette recherche incarne le type d'activité humaine rationnelle qui seule peut apporter la bonne vie et le bonheur authentique. (185)
Pour Aristote, le but de la vie est le bonheur et les mathématiques encouragent la reconnaissance du chemin vers ce but. Que ce soit dans sa Métaphysique, où il explique les mathématiques de la symétrie et la manière dont elles reflètent la beauté, ou dans son Éthique à Nicomaque , où il prône l'équilibre personnel par le biais du nombre d'or, les mathématiques informent la pensée d'Aristote autant que celle de Platon. Aristote consacra toutefois beaucoup plus de temps aux mathématiques pratiques que son maître, comme le firent de nombreux mathématiciens après lui.
Euclide, Archimède, Ératosthène et autres
Les Éléments d'Euclide, certainement le livre le plus vendu dans l'histoire du monde avant que la Bible ne prenne ce titre, codifient, expliquent et développent les mathématiques en 13 volumes couvrant les constructions pythagoriciennes, le parallélisme, le nombre d'or, le théorème de Thalès, les nombres premiers, les cônes, les pyramides, l'optique, les sphères, et définissent ce que l'on appelle aujourd'hui la géométrie euclidienne. Son travail eut une telle influence et devint si populaire que Ptolémée Ier Soter (r. de 323 à 282 av. J.-C.) d'Égypte invita Euclide à sa cour pour discuter des Éléments. L'érudit Lionel Casson commente:
[Ptolémée Ier] devait au moins avoir tâté des mathématiques, car c'est lui qui, en demandant à Euclide s'il n'existait pas un moyen plus court d'apprendre la géométrie que les Éléments, obtint la célèbre réponse : "Il n'y a pas de voie royale." (32)
Ptolémée Ier créa la bibliothèque d'Alexandrie, construite sous le règne de Ptolémée II Philadelphe (282-246 av. J.-C.), qui devint un point de repère pour les plus grands esprits de l'époque. Parmi eux, Archimède de Syracuse, le plus grand mathématicien grec, reconnu aujourd'hui comme le plus important de l'Antiquité. Archimède est connu comme le "père des mathématiques" pour ses contributions à la discipline, notamment l'équilibre des plans, la mesure des cercles, les théorèmes mécaniques, la mesure des sphères et des cylindres, l'équilibre des plans, la parabole, l'ellipse, l'aire d'une spirale, le concept de flottabilité, l'invention de la vis d'Archimède basée sur des principes mathématiques, et l'invention de la poulie et du levier à l'aide de la même vis. On dit qu'il est mort alors qu'il était préoccupé par une équation mathématique et qu'il aurait ignoré l'ordre du soldat romain qui le tua.

Ératosthène, un polymathe, était l'un des bibliothécaires en chef de la bibliothèque d'Alexandrie. Il fut le premier à calculer la circonférence de la terre et à rédiger une géographie complète du monde connu. On lui attribue même la paternité du terme "géographie". Ses calculs astronomiques furent ensuite utilisés par Hipparque de Nicée, considéré comme le plus grand astronome de son époque. Aristarque de Samos s'appuya sur les développements mathématiques de ses prédécesseurs pour parvenir à son modèle héliocentrique de l'univers, qui ne fut rejeté par Hipparque que parce qu'il contredisait le modèle accepté à l'époque, tel qu'il avait été établi par Aristote, considéré comme l'autorité en la matière, ainsi que dans bien d'autres domaines. Claude Ptolémée, dans son Almageste, distilla les données astronomiques du passé et y ajouta ses propres observations, créant ainsi un ouvrage qui allait influencer Nicolaus Copernic (1473-1543) et inspirer la révolution scientifique du début de l'ère moderne.
Conclusion
La Mésopotamie, l'Égypte ancienne, la civilisation de la vallée de l'Indus et la Chine ancienne avaient développé des principes mathématiques bien avant l'époque de Thalès de Milet. Le terme "histoire ancienne" ne semble pas si ancien lorsqu'il s'applique à la prédiction de l'éclipse par Thalès en 585 avant notre ère, si l'on comprend que les astronomes d'autres civilisations avaient fait de même plus de 2 000 ans auparavant. Hippocrate, reconnu comme le "père de la médecine", était en fait un retardataire dans ce domaine; Sushruta (vers le 7e/6e siècle av. J.-C.) de l'Inde ancienne pratiquait la chirurgie et rédigeait des journaux médicaux des siècles avant même la naissance d'Hippocrate.
Cela n'enlève rien à la contribution des mathématiciens grecs. L'érudit Thomas Cahill fait remarquer:
Il est important [...] de rappeler que la question sous-jacente pour tous [les philosophes / mathématiciens grecs] - "Quelle est la nature de la réalité ?" - reste à ce jour une question fondamentale à laquelle chacun d'entre nous doit tenter de répondre dans sa vie. Lorsque nous nous souvenons de cela et que nous reconnaissons le peu de progrès que nous avons réalisé dans la formulation d'une réponse satisfaisante, nous éprouvons une certaine sympathie pour eux et pour l'acharnement avec lequel ils ont abordé leur tâche intimidante. Parce qu'ils n'avaient aucune ligne directrice à suivre, ils ont mis leur nez partout dans l'espoir de trouver une réponse adéquate et, ce faisant, ils ont contribué à inventer les disciplines de la philosophie, de la théologie, des sciences physiques, de la médecine, de la psychologie, de la science politique et de l'éthique. (151)
Les Grecs n'ont inventé aucune de ces disciplines, mais leur développement des concepts de chacune d'entre elles a jeté les bases sur lesquelles d'autres se sont appuyés pour faire progresser la civilisation occidentale. Lorsque l'on utilise son smartphone ou que l'on cherche sur son ordinateur personnel une recette pour le dîner, on doit remercier les mathématiciens grecs pour ce genre de luxe, pour cela et pour bien d'autres choses encore.