Greek mathematics, the study of numbers and their properties, patterns, structure, space, apparent change, and measurement, is said to have originated with Thales of Miletus (l. c. 585 BCE) but was clearly understood during the periods of the Minoan civilization (2000-1450 BCE) and the Mycenaean Civilization (c. 1700-1100 BCE) and was derived from older Mesopotamian and Egyptian mathematical systems.

These systems, however, served practical purposes, as noted by scholar Rosalie David:
Mathematics served basically utilitarian purposes in Egypt and does not seem to have been regarded as a theoretical science. (217)
Scholar Gwendolyn Leick says the same regarding Mesopotamian mathematics:
Mathematics was an integral part of scribal training and practice tablets from as early as the Early Dynastic Period demonstrate that geometry was essential for the task of dividing up plots of land for farming and irrigation purposes. (116)
Thales, and the other great early mathematician Pythagoras (l. c. 571 to c. 497 BCE, best known for the Pythagorean Theorem), viewed mathematics as a means for apprehending truth, elevating it from the level of a simple pragmatic instrument to the basis for understanding reality. None of Thales' writings have survived, but he is considered the first mathematician of Greece for introducing geometry and, it seems, for how he applied it. Pythagoras, possibly one of his students, made mathematics central to his philosophy which advocated, among other things, reincarnation in the belief that the soul, like numbers, was eternal and returned after death in other and still other forms.
Among the students of Pythagoras was Hippasus of Metapontum (l. c. 530 to c. 450 BCE), credited with discovering irrational numbers, and his work was further developed by Theodorus of Cyrene (l. 5th century BCE). Another Pythagorean, Philolaus of Croton (l. c. 470 to c. 385 BCE) developed the pyrocentric model of the universe and was the teacher of the great mathematician Archytas of Tarentum (l. 5th century BCE). Archytas, in turn, was the teacher of Eudoxus of Cnidus (l. c. 408 to c. 355 BCE), also famous as a brilliant mathematician and astronomer.
These mathematicians influenced the works of Plato (l. 424/423-348/347 BCE) and Aristotle (l. 384-322 BCE), whose philosophies were informed by mathematics, notably geometry. Euclid (l. c. 300 BCE) established geometry through his famous Elements and is known as the "Father of Geometry." The best-known Greek mathematician is the inventor and engineer Archimedes of Syracuse (l. 287-212 BCE), but other notables include Eratosthenes (l. c. 276-195 BCE), Apollonius of Perga (l. c. 240 to c. 190 BCE), Aristarchus of Samos (l. c. 310 to c. 230 BCE), Hipparchus of Nicea (l. c. 190 to c. 120 BCE), Menelaus of Alexandria (l. c. 100 CE), and Claudius Ptolemy (l. 100-170 CE). These thinkers lay the foundation that was developed further by later mathematicians, preserving and advancing their work, which allowed for mathematical progress into the modern era.
Stolen Legacy Claim
The Sumerians of Mesopotamia had already developed sophisticated mathematics by the Early Dynastic Period (2900-2334 BCE) with a sexagesimal place notation of 60. This enabled them to create the concept presently recognized as 'time' based on the concept of 60, which defines a minute as 60 seconds and an hour as 60 minutes. The Sumerian system provides evidence of an understanding of addition, subtraction, multiplication, division, algebra, geometry, reciprocals, squares, and quadratic equations. The Egyptians, more practical and conservative, worked in addition, subtraction, multiplication, and division with elements of calculus and, perhaps, algebra.
As noted, the Mesopotamians and Egyptians used mathematics for practical purposes. Rosalie David elaborates:
The Egyptians certainly possessed an organized system of mathematical knowledge, but they used practical experience rather reasoning skills to solve problems. Although they started with elementary concepts, they soon developed systems that coped with some complicated arithmetical and geometrical problems, and they made use of fractions. (218)
It is therefore inaccurate to claim the Greeks invented mathematics, though this assertion has been advanced for centuries, and more precise to say they developed mathematical concepts further than earlier civilizations. Even though Sumerian mathematics was highly advanced, it was nowhere near as refined as Greek mathematics from the 6th century BCE going forward. The Pythagorean Theorem, for example, was known to the Babylonians long before Pythagoras was even born, but his definition not only preserved but also seems to have refined the concept.

Even so, the claim that Greek mathematics and Greek philosophy were somehow 'stolen' from earlier civilizations is also inaccurate and an oversimplification that ignores actual history. Egyptian hieroglyphics and Mesopotamian cuneiform were not deciphered until the mid-to-late-19th century, and, by that time, a significant body of historical work had been created by European scholars who only knew history through what was available to them: Greek and Latin sources. The 'decorations' noted on ancient Mesopotamian and Egyptian temples, tombs, and inscriptions were not recognized as writing systems – nor was there any way they could have been – as they had not yet been deciphered by c. 1820.
Many of the conclusions the early modern and modern-era scholars came to regarding ancient history now need revision – and there were, no doubt, racialized motives at work in the interpretation of data – but, overall, they did not intentionally sideline earlier civilizations to favor the Greeks; they were simply unaware of Mesopotamian and Egyptian history. If one believes, according to the survey one had done, that one's property covers X number of feet, and is later informed by one's neighbor that he actually owns those feet, one cannot be accused of stealing land; only of being misinformed. If one does not respect and respond to the new information, only then can one be said to be at fault.
Greek mathematics, then, acknowledged as based on earlier systems, dates to the 6th century BCE. The Minoan and Mycenean systems were lost during the Greek Dark Age and have not been reconstructed. Thales of Miletus, therefore, is generally understood as the first to introduce theoretical mathematics to Greece, even though the discipline existed prior to his time in other regions.
Pre-Socratic Philosophers & Pythagoreans
Thales is the first of the so-called Pre-Socratic Philosophers, the term given to the thinkers who lived in Greece before the time of Socrates of Athens (470/469-399 BCE), and so is known as the first philosopher of ancient Greece. According to the works of later Greek writers, he seems to have followed the same paradigm as the Babylonians and Egyptians at first in using mathematics for practical ends. He is said, for example, to have measured the height of the pyramids of Giza by calculating the difference between their shadows and his own and, applying mathematical principles to a logistical problem, diverted the course of the Halys River so the army of King Croesus (r. 560-547 BCE) could cross when he was employed by Croesus as an engineer.
In time, however, his mathematics became more theoretical as he proposed axioms, proofs, defined the meaning of number, developed geometry, proposed the so-called Thales' Theorem (to find the center of a circle), and applied mathematics to astronomy, accurately predicting the solar eclipse of 28 May 585 BCE.
Pythagoras, however (another Pre-Socratic philosopher), developed mathematics further as a course of study. The later writer Proclus notes how "Pythagoras turned geometrical philosophy into a form of liberal education by seeking its first principles in a higher realm of reality" (Baird, 16). To Pythagoras, mathematics was a means to an end but was also the end itself. The early Pre-Socratics were concerned with finding the First Cause of existence, proposing water, air, fire, or otherworldly elements, but Pythagoras claimed that mathematics explained the visible and invisible world because numbers, like creation, have no beginning or end.
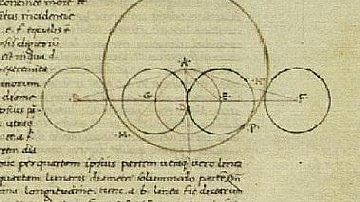
Number, to Pythagoras, was the First Cause because it could be proven that the many can come from the one – the plurality observed in the world could, and did, arise from a single source. Pythagoras' concept of number was based on a dot in the center of a circle – the monad, which stood for the concept of One, of unity. From the monad, came the dyad, two circles now sharing a common center and, by drawing a line horizontally across their intersection, an equilateral triangle is formed, shifting the dyad to a triad and so on through the decad. From the One, therefore, came the many and, although numbers might seem limited in sequence running between 1-10, they were actually limitless in the combinations of that sequence running 11-20, then 21-30, and so on forever.
Pythagoras applied the eternal nature of number to the human soul, arguing that one's spirit, like a number, returned again and again after bodily death in different forms – like the sequence of numbers – now appearing as a human being, now as a dog, or a mule, or a housefly. Accordingly, Pythagoras advocated vegetarianism because there was no way of knowing if the animal one slaughtered might not be one's departed uncle or father in the body of a chicken.
Pythagoras' student Philolaus of Croton rejected what he viewed as the nonsense of establishing a first cause and directed his energies to the mathematical examination of the cosmos, eventually concluding that Earth (and all the other planets as well as the sun) revolved around a central, limitless fire, contradicting the accepted model of the day that Earth was the center of the universe. He rejected the Milesian school of Thales and his followers Anaximander and Anaximenes that insisted on the importance of the First Cause in favor of a more practical use of philosophy in recognizing how the observable world works. Scholar Robin Waterfield comments:
[To Philolaus], the true essence of things is accessible only to the gods, or perhaps to a man with divine knowledge; and in the nature of things, we cannot know the infinite. In part, Philolaus is here criticizing the Milesians or similar attempts to divine an ultimate reality behind the things of this world. He is suggesting that this is impossible, and that the best one can do, instead, is to try to say what the necessary preconditions are for the world we are faced with to exist. (93)
Archytas adopted Philolaus' approach and also applied mathematics to understanding the form of the world and how it worked. Archytas, in fact, is said to have been greatly admired by Plato for his ability to combine philosophic idealism with practical application. Archytas was not only a general of Tarentum, elected seven years in a row and considered invincible but is also known as the founder of mathematical mechanics, is famous for solving the geometric problem known as "doubling the cube", and was renowned in his lifetime for his contributions to astronomy and music theory.
Plato & Aristotle
Although Plato is not usually included in lists of Greek mathematicians, the underlying form of his philosophy was mathematics and, specifically, pure geometry. Plato rejected the relativism championed by Sophists like Protagoras of Abdera (l. c. 485-415 BCE), who claimed, "of all things a man is the measure" – that the individual alone defined truth – and insisted on universal, eternal truths that informed what was recognized as 'truth' on earth. To Plato, something was not 'true' just because one believed it so; it was 'true' in so far as it participated in the Form of Truth in a higher realm. Geometry, Plato felt, established these higher truths, calmed the passions, cleared the mind, and freed one from the 'true lie' or 'the lie in the soul' that caused one to believe wrongly about the most important aspects of life.
Aristotle, (Plato's most famous student) on the other hand, is famous for his contributions to Greek mathematics. Scholar Thomas R. Martin writes:
Aristotle regarded science and philosophy not as abstract subjects isolated from the concerns of ordinary existence but rather as the disciplined search for knowledge in every aspect of life. That search epitomized the kind of rational human activity that alone could bring the good life and genuine happiness. (185)
To Aristotle, the purpose of life was happiness and mathematics encouraged one's recognition of the path toward this goal. Whether in his Metaphysics, where he explains the mathematics of symmetry and how it reflects beauty, or in his Nicomachean Ethics, where he advocates for personal balance through his Golden Mean, mathematics informs Aristotle's thought as much as it did Plato's. Aristotle, however, devoted considerably more time to practical mathematics than his teacher, as would many of the mathematicians who came after him.
Euclid, Archimedes, Eratosthenes & Others
Euclid's Elements, easily the bestselling book in the history of the world before the Bible took that title, codified, explained, and expanded upon mathematics in 13 volumes covering Pythagorean constructs, parallelism, the golden ratio, Thales' Theorem, prime numbers, cones, pyramids, optics, spheres, and defined what has come to be known as Euclidian Geometry. His work was so influential and became so popular that Ptolemy I Soter (r. 323-282 BCE) of Egypt invited Euclid to his court to discuss Elements. Scholar Lionel Casson comments:
[Ptolemy I] must have at least dabbled in mathematics, for it was he who, on asking Euclid whether there wasn't a shorter way to learn geometry than through The Elements, got the celebrated reply, "There is no royal road." (32)
Ptolemy I established the Library of Alexandria, which was built during the reign of Ptolemy II Philadelphus (282-246 BCE) and became a beacon for the greatest minds of the age. Among these was Archimedes of Syracuse, the greatest Greek mathematician and recognized today as the most significant in antiquity. Archimedes is known as the "Father of Mathematics " for his contributions to the discipline, including the equilibrium of planes, measurement of circles, mechanical theorems, measurement of spheres and cylinders, equilibrium of planes, the parabola, the ellipse, the area of a spiral, the concept of buoyancy, the invention of the Archimedes Screw based on mathematical principles, and the invention of the pulley and lever using the same. He is said to have died while preoccupied with a mathematical equation and so ignored the command of the Roman soldier who killed him.
Eratosthenes, a polymath, was one of the head librarians at the Library of Alexandria and the first to calculate the circumference of the earth and write a comprehensive geography of the known world. He is even credited with coining the term 'geography.' His astronomical calculations were later used by Hipparchus of Nicea, regarded as the greatest astronomer of his age. Aristarchus of Samos drew on the mathematical developments of his predecessors to arrive at his heliocentric model of the universe, only dismissed by Hipparchus because it contradicted the accepted model of the time as set down by Aristotle, considered the authority on that subject as well as many others. Claudius Ptolemy, in his Almagest, distilled the astronomical data of the past and contributed his own observations, creating a work that would influence Nicolaus Copernicus (l. 1473-1543) and inspire the Scientific Revolution of the Early Modern Era.
Conclusion
Mesopotamia, ancient Egypt, the Indus Valley Civilization, and ancient China, had developed mathematical principles long before the time of Thales of Miletus. The term 'ancient history' does not seem so ancient as applied to Thales' prediction of the eclipse in 585 BCE when one understands that the astronomers of other civilizations had been doing the same over 2,000 years before. Hippocrates, recognized as the "Father of Medicine" was actually a latecomer to the field; Sushruta (l.c. 7th/6th century BCE) of ancient India was practicing surgery and writing medical journals centuries before Hippocrates was even born.
Even so, this does not detract from the contributions of the Greek mathematicians. Scholar Thomas Cahill notes:
It is important…to recall that the underlying question for all [of the Greek philosophers/mathematicians] – "What is the nature of reality?" – remains to this day a fundamental question that each of us must attempt to answer in our lives. When we recall this – and acknowledge how little progress we have made in formulating a satisfactory answer – we gain a measure of sympathy for them and the single-minded spunk with which they approached their daunting task. Because they had no guidelines to follow, they poked their noses into everything in the hopes of finding an adequate answer; and in the process they helped to invent the disciplines of philosophy, theology, the physical sciences, medicine, psychology, political science, and ethics. (151)
The Greeks did not actually invent any of these, but their development of the concepts of each lay the groundwork for others to build on in the progress of Western Civilization. When one uses one's smartphone or searches one's personal computer for a recipe for dinner, one has the Greek mathematicians to thank for that kind of luxury; for that, and so much more.